MSCKF算法学习
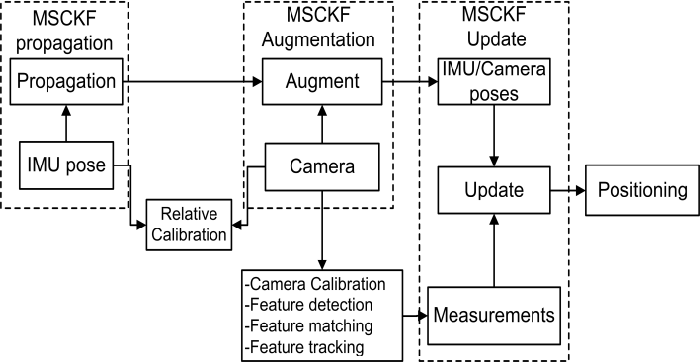 Structure of MSCKF
Structure of MSCKF
VIO 简介
VIO 分类
- 紧耦合(tightly-coupled): 紧耦合需要把图像feature(特征点)加入到状态向量中去,因此整个系统状态向量的维数会非常高,因此也就需要很高的计算量。比较经典的算法是MSCKF,ROVIO,紧耦合的另外一个优点是 IMU 的尺度度量信息可以用于辅助视觉中的尺度的估计
- 松耦合(loosely-coupled): 松耦合的方法相比紧耦合则简单的多,松耦合算法避免把图像的feature加入状态向量,而是把图像当成一个black box,计算vo处理之后才和imu数据进行融合
简而言之,松耦合就是指IMU和相机分别进行自身的运动估计,然后对其位姿估计结果进行融合,而紧耦合是指把IMU的状态与相机的状态合并在一起,共同构建运动方程和观测方程,然后进行状态估 计。

VIO算法的好处
- 恢复尺度: IMU能够提供尺度信息(加速度计),解决单目VO的无法恢复尺度的问题。
- 应对纯旋转: 在纯旋转的情况下,VO位姿解算会出现奇异,VIO可以利用IMU的陀螺仪(角速度计)来估计纯旋转运动。
- 应对纯旋转: 在纯旋转的情况下,VO位姿解算会出现奇异,VIO可以利用IMU的陀螺仪(角速度计)来估计纯旋转运动。
- 精度更高: VIO融合了两种传感器的信息,位姿估计的精度要更高。
VIO算法分类
graph TD;
VIO-->松耦合;
VIO-->紧耦合;
紧耦合-->基于优化的算法;
紧耦合-->基于滤波的算法;
基于优化的算法-->OKVIS;
基于优化的算法-->VINS;
基于滤波的算法-->ROVIO;
基于滤波的算法-->MSCKF;
MSCKF
MSCKF 简介
MSCKF 全称 Multi-State Constraint Kalman Filter(多状态约束下的Kalman滤波器),是一种基于滤波的VIO算法,2007年由Mourikis在《A Multi-State Constraint Kalman Filter for Vision-aided Inertial Navigation》中首次提出。MSCKF在EKF框架下融合IMU和视觉信息,相较于单纯的VO算法,MSCKF能够适应更剧烈的运动、一定时间的纹理缺失等,具有更高的鲁棒性;相较于基于优化的VIO算法(VINS,OKVIS),MSCKF精度相当,速度更快,适合在计算资源有限的嵌入式平台运行。在机器人、无人机、AR/VR领域,MSCKF都有较为广泛的运用,如Google Project Tango就用了MSCKF进行位姿估计。
MSCKF核心思想
MSCKF的目标是解决EKF-SLAM的维数爆炸问题。传统EKF-SLAM将特征点加入到状态向量中与IMU状态一起估计,当环境很大时,特征点会非常多,状态向量维数会变得非常大。MSCKF不是将特征点加入到状态向量,而是将不同时刻的相机位姿(位置 $p$ 和姿态四元数 $q$ )加入到状态向量,特征点会被多个相机看到,从而在多个相机状态(Multi-State)之间形成几何约束(Constraint),进而利用几何约束构建观测模型对EKF进行update。由于相机位姿的个数会远小于特征点的个数,MSCKF状态向量的维度相较EKF-SLAM大大降低,历史的相机状态会不断移除,只维持固定个数的的相机位姿(Sliding Window),从而对MSCKF后端的计算量进行限定。
EFK-SLAM 与 MSCKF 的状态向量对比
$$X_{{EKF-SLAM}} = [X_{IMU},f_1,f_2,f_3,\cdots,f_M]$$ $$X_{MSCKF} = [X_{IMU},p_{c1},q_{c1},p_{c2},q_{c2},p_{c3},q_{c3},\cdots,p_{cN},q_{cN}]$$
背景知识1
旋转量求导
一个刚体在同一个惯性坐标系下进行平移运动,其平移量对时间的一阶导和二阶导即速度和加速度:
$$\dot{\bf p}={\bf v} \rightarrow \dot{\bf v} = {\bf a}$$
相同的道理可以迁移到旋转量,只是对于旋转量以及非惯性系参考坐标系,情况稍微复杂些。
首先,如图2左半部所示,考虑一个从原点出发的向量 $\bf r$ 绕单位轴 $\bf u$ 旋转,角速度大小为 $\bf r$

角速度矢量可以表示为 ${\boldsymbol \omega}=\dot{\theta}\bf u$
从而表示向量 $\bf r$ 末端点 $P$ 的速度矢量,即对向量 $\bf r$ 求一阶导所得:
$$ \frac{d{\bf r}}{dt} = {\boldsymbol \omega} \times {\bf r} $$
现在考虑图2右侧:表示坐标系 $B$ 绕单位轴 $\bf u$ 旋转,和上面同理,其三个轴的时间一阶导同样为
$$\frac{d{\bf i}_B}{dt} = {\boldsymbol \omega} \times {\bf i}_B, \frac{d{\bf j}_B}{dt} = {\boldsymbol \omega} \times {\bf j}_B, \frac{d{\bf k}_B}{dt} = {\boldsymbol \omega} \times {\bf k}_B$$
因为 $[ {\bf i}_B \quad {\bf j}_B \quad {\bf k}_B ]$ 实际上是坐标系 $B$ 相对于参考坐标系的旋转矩阵 $\bf R$ 。所以 $\bf R$ 的时间一阶导为
$$\dot{\bf R} = [ {\boldsymbol \omega} \times {\bf i}_B \quad {\boldsymbol \omega} \times {\bf j}_B \quad {\boldsymbol \omega} \times {\bf k}_B ] = {\boldsymbol \omega} \times {\bf R} \tag{1.0} $$
我们知道上面的叉乘运算可以转化为负对称(skew symmetric)矩阵的乘法:
$$\dot{\bf R} = {\boldsymbol \omega}^{\land} {\bf R}\tag{1.1}$$
其中负对称矩阵为
$$\quad {\boldsymbol \omega}^{\land}= \begin{bmatrix}0 & -\omega_3 & \omega_2\\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0\end{bmatrix}$$
角速度也经常表达在体坐标系 $B$ 下,记为 ${}^B{\boldsymbol \omega} = {\bf R}^T{\boldsymbol \omega}$,即 ${\boldsymbol \omega} = {\bf R}{}^B{\boldsymbol \omega}$,于是 $(1.1)$ 可以写作
$$ \dot{\bf R} = ({\bf R}{}^B{\boldsymbol \omega})^{\land} {\bf R} \tag{1.2}$$
这里我们要利用负对称矩阵的一个很好的性质:对任意旋转矩阵 $\bf R$ 和三维向量 $\bf v$,都有 $({\bf R v})^{\land} = {\bf Rv^{\land}R}^T$(参看《 (Rv)^ = Rv^R’ 的简单证明》),于是 $(1.2)$ 可以写成
$$ \dot{\bf R} = {\bf R}({}^B{\boldsymbol \omega})^{\land} \tag{1.3} $$
比较一下 $(1.1)$ 和 $(1.3)$,可以发现一个很有趣的事实,角速度如果表达在参考坐标系下,负对称矩阵写在左边;如果表达在体坐标系下,负对称矩阵写在右边。这点微小的区别,读者在阅读文献时可以特别留意。
四元数
这部分讲四元数如何表示旋转的前置知识,熟悉的读者可以跳过。
用旋转矩阵来表示旋转很直观,但过于冗余,因为旋转只有三个自由度,而旋转矩阵有九个量。表征旋转还可以用欧拉角,但有万向锁问题,而且计算也不方便。旋转向量(即李代数 $so(3)$)和四元数是更常用的表征方法,在惯性导航中四元数似乎更普遍些。这里采用四元数。
一个四元数由一个实部和三个虚部构成,书写顺序各家不同,这里和 MSCKF 2 一样,虚部在前实部在后:
$$ {\bf q} = q_1 i + q_2 j + q_3 k + q_4 = [{\boldsymbol v}^T \quad q_4]^T$$
虚部 ${\boldsymbol v}=[q_1 \quad q_2 \quad q_3]^T$。虚部三个基 $i,j,k$ 满足 $i^2=j^2=k^2=ijk=-1$。 四元数仍是一种冗余表达法,为了更紧凑,通常使用使用单位四元数 $\bar{\bf q}$,通过将四元数的模置为 1 得到。
四元数和旋转向量有很直接的转换关系。绕单位轴 $\bf u$ 转了 $\theta$ 角度,用四元数表达为
$$ {\bf q} = [{\bf u}\sin\frac{\theta}{2} \quad \cos\frac{\theta}{2}] \tag{1.4}$$
四元数乘法 $\otimes$ 为类似于多项式乘法的逐项相乘:
$$ \begin{aligned} {\bf q}\otimes {\bf p} = & (q_1 i + q_2 j + q_3 k + q_4)(p_1 i+p_2j+p_3k+p_4) \\ = & (q_1p_4+q_2p_3-q_3p_2+q_4p_1)i+(-q_1p_3+q_2p_4+q_3p_1+q_4p_2)j+\\ &(q_1p_2-q_2p_1+q_3p_4+q_4p_3)k + (-q_1p_1-q_2p_2-q_3p_3+q_4p_4) \end{aligned} $$
这个计算结果可以表达为多种形式:
$$ \begin{aligned} {\bf q}\otimes {\bf p} & = \begin{bmatrix} q_4{\bf I}_3+{\boldsymbol v}_q^{\land} & {\boldsymbol v}_q \\ -{\boldsymbol v}_q^T & q_4 \end{bmatrix} \begin{bmatrix} {\boldsymbol v}_p \\ p_4 \end{bmatrix} \\ & = \begin{bmatrix} p_4{\bf I}_3-{\boldsymbol v}_p^{\land} & {\boldsymbol v}_p \\ -{\boldsymbol v}_p^T & p_4 \end{bmatrix} \begin{bmatrix} {\boldsymbol v}_q \\ q_4 \end{bmatrix} \end{aligned} $$
四元数乘法和其对应的两个旋转矩阵相乘物理意义是一样的,即 ${\bf R}({\bf q\otimes p})={\bf R}({\bf q}){\bf R}({\bf p})$。四元数对应的旋转矩阵为:
$$ {\bf R}({\bf q}) = (2q_4^2-1){\bf I}_3 +2q_4{\boldsymbol v}^{\land} + 2{\boldsymbol{vv}}^T \tag{1.5}$$
四元数的逆为 ${\bf q}^{-1} = [-{\boldsymbol v}^T \quad q_4]^T$。易得 ${\bf q}\otimes{\bf q}^{-1}=[0\quad 0\quad 0\quad 1]^T:={\bf q}_I$,故 ${\bf q}_I$ 表示旋转量为零。
四元数对时间一阶导为
$$\begin{align} \dot{\bf q} &= \frac{1}{2} \begin{bmatrix} {\boldsymbol \omega}^{\land} & {\boldsymbol\omega} \\ -{\boldsymbol \omega}^T & 0 \end{bmatrix} {\bf q} := \frac{1}{2}{\boldsymbol \Omega}({\boldsymbol \omega}){\bf q} \tag{1.6} \\ &= \frac{1}{2} \begin{bmatrix} q_4{\bf I}_3-{\boldsymbol v}^{\land} \\ -{\boldsymbol v}^T \end{bmatrix} {\boldsymbol \omega} \end{align}$$
读者可能注意到了 $(1.6)$ 和 $(1.1)$ 形式上的相似。这里 $\boldsymbol \omega$ 的意义也是一样的。$(1.6)$ 的推导可以参考3,这里不赘述。
IMU 模型
如果背景知识忘记了,可以查阅 背景知识
IMU 状态模型
IMU 是移动机器人、移动智能设备上常见的传感器。常见的IMU为六轴传感器,配备输出三轴加速度的加速度计和输出三轴角速度的陀螺仪。九轴IMU还会配备输出三轴姿态角的磁力计,我们这里只讨论六轴IMU。
IMU 的状态量通常表示为:
$${\bf X}_{IMU} = [ {}^I_G \bar{q}^T \quad {\bf b}_g^T \quad ^G{\bf v}_I^T \quad {\bf b}_a^T \quad ^G{\bf p}_I^T] $$
这里用$I$表示IMU坐标系,$G$表示参考坐标系。IMU 的姿态由旋转量 ${}^I_G \bar{q}$ 和平移量 $^G{\bf p}_I$ 表示, 更具体来说,前者是将任意向量从 $G$ 坐标映射到 $I$ 坐标的旋转量,用单位四元数表示;后者为 IMU 在 $G$下的三维位置。$^G{\bf v}_I$是IMU 在 $G$坐标系下的平移速度。另外两个量 ${\bf b}_g$ 和 ${\bf b}_a$ 表示陀螺仪(角速度计)和加速度计的 bias。
这里除了 bias 之外的状态量是包含时间维度信息的:
平移量表达到速度(p 和 v,对时间的一阶导),因为 IMU 只提供到加速度(对时间的二阶导)的测量;旋转量只表达姿态量(对时间的零阶导),因为 IMU 提供到角速度(对时间的一阶导)。状态量的估计可以由 IMU 测量积分得到。
小结
${}^I_G \bar{q}$ 为单位四元数,表示从世界(Global)系( $G$系 )到IMU坐标系( $I$ 系)的旋转
$b_{g}^T$ 为陀螺仪gyroscope的bias
${}^{G}v_{I}^T$ 为IMU在G系下的速度
$b_{a}^T$ 为加速度计accelerator的bias
${}^{G}p_{I}^T$ 为IMU在G系下的位置
对于 IMU 状态估计问题,需要提供运动模型、观测(噪声)模型、估计误差模型:
$$\dot{\bf x} = f({\bf x})$$ $${\bf z} = g({\bf x}) + {\bf n}$$ $$\delta {\bf x} = e(\hat{\bf x},{\bf x})$$
这是一个通用模型,我们用 $x$ 表示真实状态量(待估计,不可知),用 $z$ 表示观测量,$n$ 表示观测噪声,$\hat{\bf x}$ 表示当前的状态估计量。
IMU 运动模型
有了前置知识的铺垫之后,我们可以给出 IMU 的运动模型:
$$ \begin{align} {}^I_G \dot{\bar{q}} &= \frac{1}{2}{\boldsymbol \Omega}({\boldsymbol \omega}){}^I_G \bar{q}\\\ \dot{\mathbf b}_g &= {\mathbf n}_{wg}\\\ {}^G\dot{\mathbf{v}}_I &= {}^G\mathbf{a} \tag{1.7}\\\ \dot{\mathbf{b}}_a &= {\mathbf{n}}_{wa} \\\ {}^G\dot{\mathbf{p}}_I &= {}^G{\mathbf{v}}_I \end{align} $$
${}^I_G \dot{\bar{q}}$ 由 $(1.6)$ 直接得到。注意这里角速度 $\boldsymbol \omega$ 是在体坐标系 {I} 下表达的,与 $(1.1)$ 处相反。原因是 ${}^I_G \bar{q}$ 表示的旋转方向与 $(1.1)$ 处的 $\bf R$ 是相反的。其他的四项,速度和加速度都很简单,bias 两项在下面观测模型部分讲。
References
-
Mourikis, Anastasios I., and Stergios I. Roumeliotis. “A multi-state constraint Kalman filter for vision-aided inertial navigation.” Proceedings 2007 IEEE International Conference on Robotics and Automation. IEEE, 2007. ↩︎
-
Trawny, Nikolas, and Stergios I. Roumeliotis. “Indirect Kalman filter for 3D attitude estimation.” University of Minnesota, Dept. of Comp. Sci. & Eng., Tech. Rep 2 (2005): 2005. ↩︎