理顺离散信号的傅里叶变换

很多控制学科的课程中都会用到一些常用的信号分析工具如傅里叶变换，Laplace变换Z变换等等。本文想着重整理一下数字信号也就是离散信号的傅里叶变换之间的关系

DTFT

DTFT (Discrete Time Fourier Transform) 适用于非周期的离散信号的频谱分析，一个离散信号的DTFT一般写为 $$X(\omega) \overset{\underset{\mathrm{def}}{}}{=} \sum_{n=-\infty}^\infty x[n]e^{-j\omega n}$$

它的反变化(IDTFT)为

$$x[n] = \frac{1}{2\pi}\int\limits_{-\pi}^\pi X(\omega)e^{j\omega n} d\omega$$

重要结论

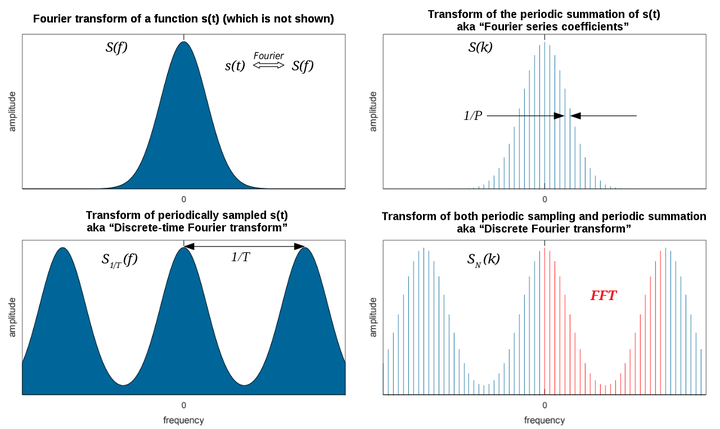
1. 连续序列的离散时间傅立叶变换(DTFT)即是采样信号的连续傅立叶变换(CFT)
2. $X(\omega)$ 是周期为 $2\pi$ 的连续时间周期信号(数学上用欧拉公式理解，物理上用aliasing理解)

为什么离散信号的频谱是连续的, aliasing 咋来的?

关于这个话题以及为什么连续信号的采样中会出现aliasing (混叠现象) 普渡大学的信号与系统课程解释的非常清晰¹，这里借用一下课程里的几幅图：

下图为对$x_4[n] = \cos(2\pi\cdot 5 \cdot T)$不同采样频率对应的频谱

下图为知识点总结 $$ \begin{array}{rcl} \fbox{离散信号 $x[n]$} & \xrightarrow{\text{的频谱是由}} & \fbox{无穷多的频率组成的} \\ \fbox{这些不同的频率部分} & \xrightarrow{\text{会造成}} & \fbox{$x[n]$信号的混叠} \end{array} $$

DFT

离散信号的傅立叶变换 DTFT，它是连续的周期函数， 尽管在理论上有重要意义，但在实际中往往难于计算。为此我们需要一种时域和频域都离散的傅里叶变换

对，这就是离散傅里叶变换 (Discrete Fourier Transformation)，简称DFT

接下来回到DFT推导，DFT说白了就是对DTFT的频谱进行采样 并截取主值 我们知道DTFT的频谱以$2\pi$为周期，设离散化后的频谱为一周期内 $N$ 个点，即$[0, 2\pi)$内有 $N$ 个点，间隔的频率 $\omega_0 = \frac{2}{N}$ ，每个采样点的频谱用 $X(k)$ 表示，则可以推出：

$$ \begin{aligned} X(k) &=\left.X(\Omega)\right|{\Omega=k \Omega{0}}=\sum_{n=-\infty}^{\infty} x[n] e^{-j k \Omega_{0} n} \\ &=\sum_{n=-\infty}^{\infty} x[n] e^{-j k \frac{2 \pi}{N} n} \\ \end{aligned} $$

其中利用$x[n]$的周期性(频域采样 时域周期延拓)：

$$e^{-j k \frac{2 \pi}{N} n}=e^{-j k \frac{2 \pi}{N}(n+r N)}$$

$$\sum_{n=1}^{N-1}\left(\sum_{r=-\infty}^{\infty} x[n+r N]\right) = x[n]$$

$$ \begin{aligned} &=\sum_{n=1}^{N-1}\left(\sum_{r=-\infty}^{\infty} x[n+r N]\right) e^{-j k \frac{2 \pi}{N} n}=\sum_{n=1}^{N-1} x_{p}[n] e^{-j k \frac{2 \pi}{N} n} \end{aligned} $$

其中

$$ x_{p}[n]=\sum_{r=-\infty}^{\infty} x[n+r N] $$

$x_p[n]$正是序列 $x(n)$ 按周期 $N$ 的延拓

---

区分DFT DTFT以及计算机是怎么用到它们的²

学过卷积，我们都知道有时域卷积定理和频域卷积定理，在这里只需要记住两点：

1. 在一个域的相乘等于另一个域的卷积；
2. 与脉冲函数的卷积，在每个脉冲的位置上将产生一个波形的镜像。

首先放上来计算机处理连续信号最终得到离散有限时域信号以及离散有限频谱的过程图，下面会分步讲解

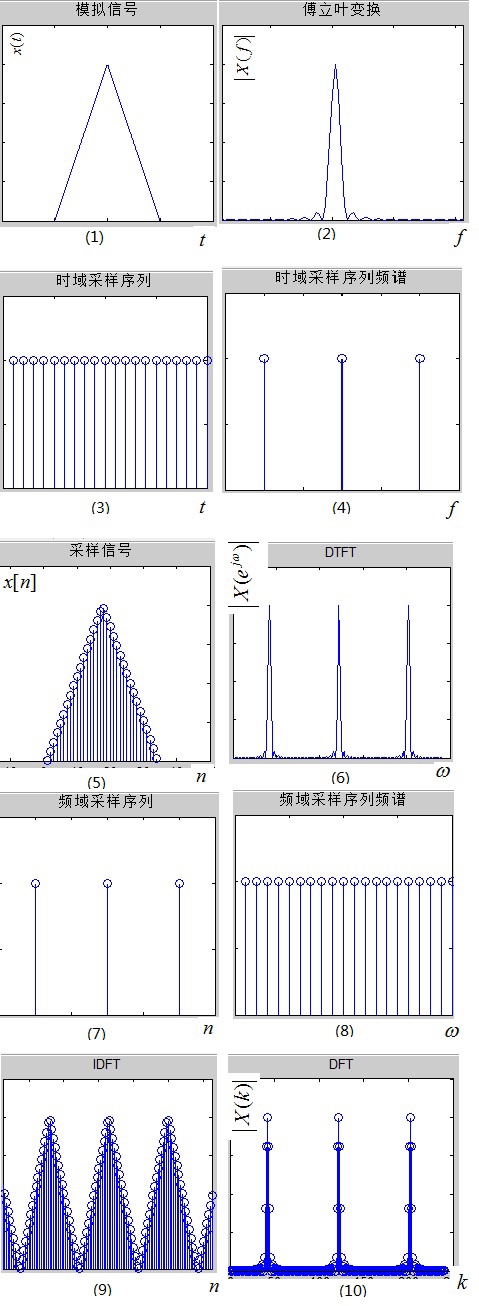
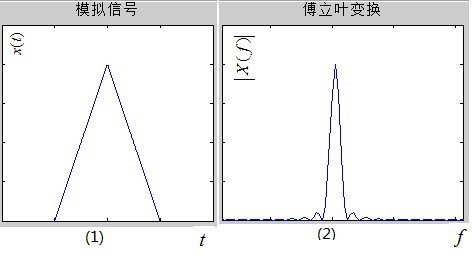
首先来说图（1）和图（2），对于一个模拟信号，如图(1)所示，要分析它的频率成分，必须变换到频域，这是通过傅立叶变换即FT(Fourier Transform)得到的，于是有了模拟信号的频谱，如图(2)

注意：时域和频域都是连续的！

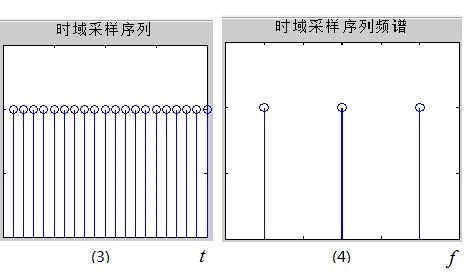
但是，计算机只能处理数字信号，首先需要将原模拟信号在时域离散化，即在时域对其进行采样，采样脉冲序列如图(3)所示，该采样序列的频谱如图(4)，可见它的频谱也是一系列的脉冲。

所谓时域采样，就是在时域对信号进行相乘，(1)×(3)后可以得到离散时间信号$x[n]$，如图(5)所示；由前面的性质1，时域的相乘相当于频域的卷积，那么，图(2)与图(4)进行卷积，根据前面的性质2知，会在各个脉冲点处出现镜像，于是得到图(6)，它就是图(5)所示离散时间信号$x[n]$ 的 DTFT(Discrete time Fourier Transform)，即离散时间傅立叶变换，这里强调的是“离散时间”四个字。

注意：此时时域是离散的，而频域依然是连续的。

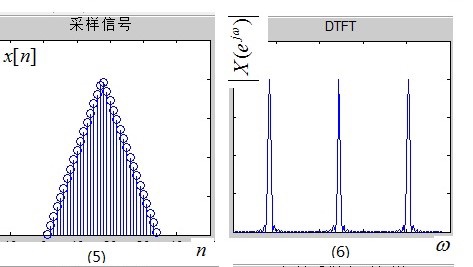
经过上面两个步骤，我们得到的信号依然不能被计算机处理，因为频域既连续，又周期。我们自然就想到，既然时域可以采样，为什么频域不能采样呢？这样不就时域与频域都离散化了吗？没错，接下来对频域在进行采样，频域采样信号的频谱如图(8)所示，它的时域波形如图(7)。

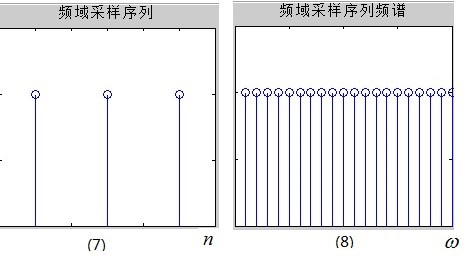
现在我们进行频域采样，即频域相乘，图(6)×图(8)得到图(10)，那么根据性质1，这次是频域相乘，时域卷积了吧，图(5)和图(7)卷积得到图(9)，不出所料的，镜像会呈周期性出现在各个脉冲点处。我们取图（10）周期序列的主值区间，并记为X(k)，它就是序列 $x[n]$ 的DFT(Discrete Fourier Transform)，即离散傅立叶变换。

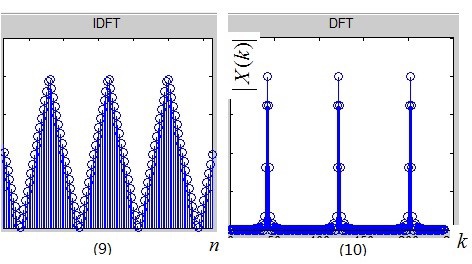
可见，DFT只是为了计算机处理方便，在频率域对DTFT进行的采样并截取主值而已。有人可能疑惑，对图(10)进行IDFT，回到时域即图(9)，它与原离散信号图(5)所示的 $x[n]$ 不同呀，它是 $x[n]$ 的周期性延拓！没错，因此你去查找一个IDFT的定义式，是不是对n的取值区间进行限制了呢？这一限制的含义就是，取该周期延拓序列的主值区间，即可还原 $x[n]$

FFT呢？FFT的提出完全是为了快速计算DFT而已，它的本质就是DFT！我们常用的信号处理软件MATLAB或者DSP软件包中，包含的算法都是FFT而非DFT。

DFS,是针对时域周期信号提出的，如果对图(9）所示周期延拓信号进行DFS，就会得到图(10)，只要截取其主值区间，则与DFT是完全的一一对应的精确关系。这点对照DFS和DFT的定义式也可以轻易的看出。因此DFS与DFT的本质是一样的，只不过描述的方法不同而已。

参考资料

• 浙江大学信号与系统ppt
• The Discrete Fourier Transform: Sampling the DTFT